Understanding variant spaces is challenging. Find out how it's made easy.

In many industries, companies have to deal with complex and variant-rich products. In the context of PLM and variant management, the question then arises as to how I can describe a product, with possibly billions and billions of possible variants, as simply and efficiently as possible.

It would be completely inefficient to try to enumerate and detail the individual variants. If there are billions and billions of possible variants of a product, it would take a very long time.

What actually is a variant space?

So we need ways to describe variant spaces. And this is where the problem begins:

What exactly is a variant space?

How can we make a variant space understandable?

When I talk about a variant space, I (usually) mean a certain number of product variants (or variants of my ‘system of interest’).

Cars, for example: You can buy them in different variants: white, green, blue, with and without a sunroof, station wagon, notchback or convertible.

...and now let's imagine a car park full of such cars 🅿🚗🚘

Sometimes "paring space" is used synonymously to "car park", so the analogy with ‘variant space’ is obvious 😉 In this car park, similar variants are close together, while dissimilar ones are further apart. So the red ones are next to each other, the green ones next to each other and the blue ones too.

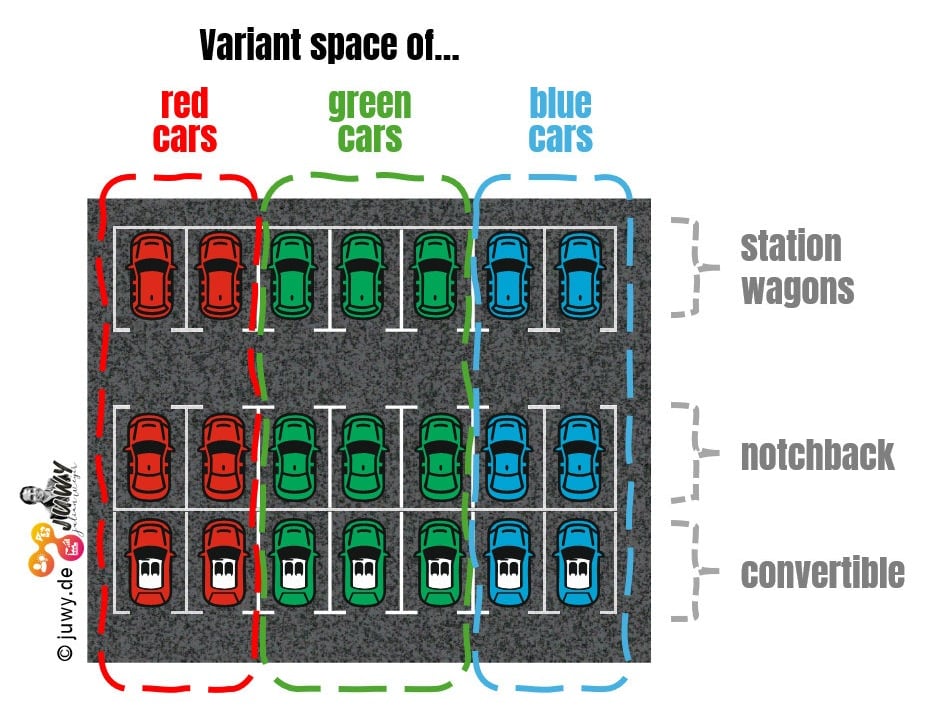
In the next row of the car park, the red, green and blue cars are again parked next to each other. However, only the station wagons are parked in the first row, the notchbacks in the second row and the convertibles in the third row.

We have already mapped two ‘dimensions’ in our car park: Colour and body type. Each property (e.g. colour), which can be different for each vehicle (red, green, blue), is a separate dimension in the variant space.

Imagine a variant space as a multidimensional multi-storey car park

The next property could be the sunroof. And either the car has a sunroof, or it doesn't (=two characteristics: present or not present). Fortunately, we can extend our car park upwards and build a two-storey car park: one floor for each characteristic of the property. The cars without sunroofs go to the top, the cars with sunroofs to the bottom.

If I am now talking about red station wagons with sunroofs, I can precisely delimit the space in this three-dimensional (variant) space in which all vehicles that correspond to these properties are parked.

And can there actually be a car in every parking space in this car park? No, it's not quite like that.

After all, convertibles with sunroofs don't really make sense, do they? The row of parking spaces in which the convertibles are parked on the upper floor simply remains empty on the lower floor. In practice, we then talk about buildability conditions, object dependencies (in SAP) or simply constraints. These ‘rules’ describe which product variants are possible or not possible. These rules do not only have to have technical reasons, but can also be defined for sales or other considerations. Perhaps, in order to optimise production, white station wagons should only be available with a sunroof.

Variation points

By the way, sometimes we talk about ‘variation points’ instead of ‘features’. And of course, the vast majority of products have more than three features or variation points (in addition to colour, design and sunroof, engine performance, comfort seats, premium or standard sat nav, auxiliary heating, etc.)

Of course, real car parks (buildings) cannot be built in more than three dimensions (not in our world, at least I have not yet seen a four-dimensional car park) - but variant spaces are fortunately only logical constructs and can in principle be described in any number of dimensions.

Back to everyday project work. How do I deal with multidimensional multi-storey car parks, sorry, variant spaces? It depends on the task, of course. Ultimately, a variant space is a set*, and everything that the mathematics of set theory has to offer can also be applied to variant spaces. Boolean algebra, arithmetic with sets, etc.

(*Is there a mathematician reading this? I'm not one, and would be grateful for any corrections or additions 😊)

Now mathematically formal-correct expressions are not everyone's cup of tea (mine only according to mood). Fortunately, in my projects it is usually sufficient to just visualise the problem and the solution. By reducing the variant spaces to two-dimensional circles (...potatoes, cucumbers, misshapen tomatoes...).

I've been doing this for a long time - at some point I learnt that this form of representation also has names in mathematics: Euler diagrams, Venn diagrams.

The quantity representation for vehicles with a glazed sunroof and auxiliary heating could then look like this, for example:

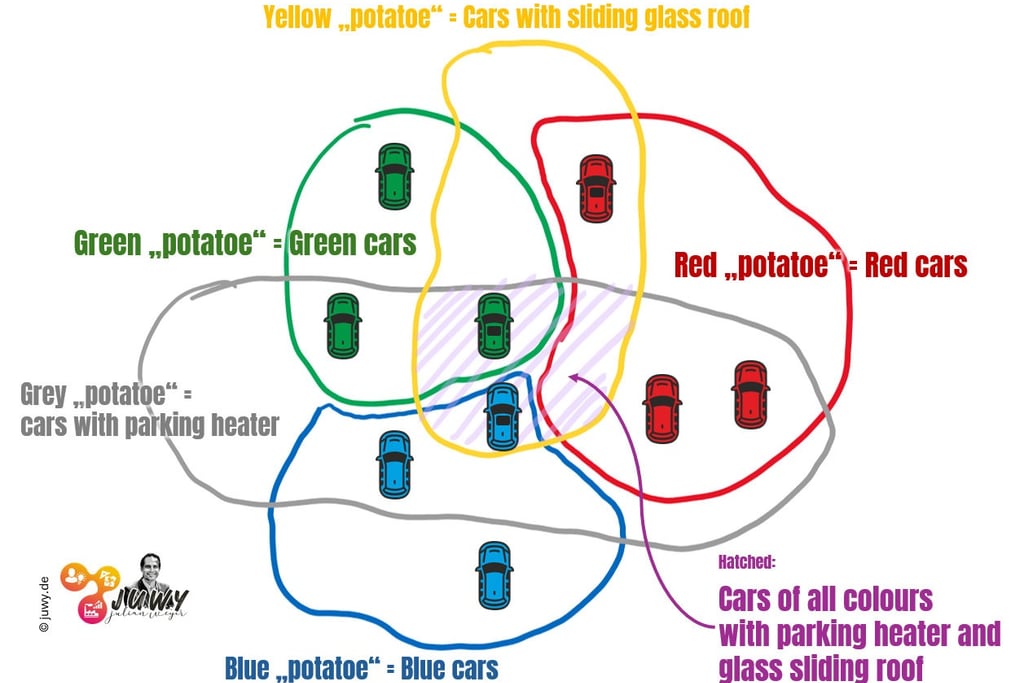
Venn unlimited

By the way, Venn has shown that, in principle, any number of sets (= any number of dimensions of the variant space) can be represented in two dimensions in a similar way. In practice, the representation of a handful of sets has been sufficient for me in every project so far, but it's good to know that there is still room for expansion 😉

"Potatoe" diagram (a.k.a. Venn diagram)

Conclusion

In my project work, I can use such representations as a basis to demonstrate principles of operation, e.g. describe algorithms for consolidating variants, how configurators are fed, which components or software are required for which variant, and much more.

And I can do this much more efficiently and comprehensibly than with linguistic descriptions or complicated mathematically correct expressions.